![]()
(1)
Базы данных: полнота и надежность
Титов В.В.
Введение
Информатизация затронула в последнее десятилетие практически все сферы нашей жизни. Переход к рыночным отношениям открыл шлюзы для свободной деятельности во всех областях, а необъятное количество и разнообразие активных и пассивных участников этой свободы породило настоятельную необходимость в упорядоченном представлении и предоставлении информации о текущем положении дел. Информация стала товаром повышенного спроса, спрос родил предложение, вслед за чем и конкуренцию. Наряду с примитивной статической информацией (монографии, газеты, рекламные и справочные издания, обклеенные стенки вагонов метро, заборов и тумб) интенсивно развивается более мобильная компьютерная информатизация, на сегодня имеющая верхом своим сеть Интернет, открывшую доступ практически ко всем информационным ресурсам мира.
Типичной упорядоченной информационной структурой является база данных. Такие базы по самым разным темам создавались еще в докомпьютерную эру, но именно компьютеризация позволила сделать качественный скачок в этом направлении: кроме собственно базы (т.е. хранилища) данных, начали интенсивно развиваться системы навигации, т.е. поиска нужных сведений в необъятном массиве базы. Все это в сочетании с повышенной потребностью в таких информационно-поисковых системах привело к появлению на рынке множества альтернативных предложений баз данных по любой более или менее интересной тематике (интересной для покупателя, конечно).
Столкнувшись с необходимостью иметь под рукой базу данных по какой-либо теме, покупатель часто оказывается озадачен тем, какую (или какие) базы ему лучше приобрести, чем та или иная база отличается от других в лучшую или худшую сторону. При этом ключевыми сравниваемыми параметрами баз данных можно считать следующие: полнота базы (т.е. наличие всех сведений по теме), качество навигационного сопровождения (т.е. легкость и точность нахождения нужной информации в базе) и оперативность обновления (т.е. темп пополнения базы свежими данными). И если два последних параметра любой пользователь может самостоятельно оценить по паспортным данным и по демонстрационной версии базы, то о полноте судить значительно труднее (хорошо, если покупатель знает десяток-другой объектов или документов, обязанных присутствовать в базе данной тематики, и может убедиться в том, сколько из них наличествует в этой конкретной базе), чаще всего единственным источником информации о полноте является честное слово разработчика базы. Однако существуют объективные методы оценки полноты баз данных, и настоящая работа посвящена одному из таких методов.
1. Расчет для двух баз данных
Исходные постулаты расчета таковы.
1. Будем называть каждый информационный объект, имеющийся в базе данных (БД), документом. Это может быть математическая формула, описание медицинского препарата, набор сведений о конкретном учебном заведении, реквизиты коммерческой фирмы, статья из научного журнала, адреса и телефоны административных учреждений, нормативный акт, и т.п., в зависимости от тематической направленности БД.
2. Каждый документ имеет набор идентификаторов, однозначно его определяющих (например, дата создания документа, создатель документа, исходящий номер, источник информации о документе, и т.п.), т.е. в любой БД наличие данного документа можно установить по комплексу его идентификаторов (в частном случае - по какому-либо одному идентификатору, если этот идентификатор - уникальный).
3. Любой документ имеет одни и те же идентификаторы в разных БД.
4. Каждая БД комплектуется документами самостоятельно, независимо от других БД, т.е. ни одна БД не является поставщиком первичной информации для другой БД.
В рамках этих положений можно далее рассуждать так.
Пусть объективно существует N документов по данной теме. Конкурирующие разработчики БД разыскивают эти документы с разной эффективностью, в результате в базе БД1 содержится
|
|
(1) |
документов, в базе БД2 -
|
|
(2) |
документов (![]() и
и ![]() - эффективность наполнения, т.е. коэффициенты полноты баз БД1 и БД2, соответственно). Сравнивая содержимое этих баз, можно обнаружить, что некоторое количество
- эффективность наполнения, т.е. коэффициенты полноты баз БД1 и БД2, соответственно). Сравнивая содержимое этих баз, можно обнаружить, что некоторое количество ![]() документов присутствует в обеих БД. Это количество (при независимости источников пополнения баз) равно:
документов присутствует в обеих БД. Это количество (при независимости источников пополнения баз) равно:
|
|
(3) |
Имея эти три уравнения, нетрудно по фактически измеренным величинам ![]() ,
, ![]() и
и ![]() вычислить три неизвестных:
вычислить три неизвестных:
|
|
|
|
(4) |
Все исходные величины (![]() ,
, ![]() и
и ![]() ) можно понимать как дискретные случайные переменные, для которых стандартное отклонение равно квадратному корню из самой величины, т.е.:
) можно понимать как дискретные случайные переменные, для которых стандартное отклонение равно квадратному корню из самой величины, т.е.:
|
|
|
|
(5) |
Относительная ошибка для этих исходных величин составляет:
|
|
|
|
(6) |
Тогда в соответствии с правилами определения относительной ошибки функции от независимых случайных величин получим для относительной ошибки a1, a2
и N следующие выражения:|
|
(7) |
|
|
(8) |
|
|
(9) |
![]() Анализируя последние три формулы, нетрудно видеть, что надежность полученных расчетных данных тем выше, чем больше каждая из трех измеренных величин. И если наименьшая из них (а это
Анализируя последние три формулы, нетрудно видеть, что надежность полученных расчетных данных тем выше, чем больше каждая из трех измеренных величин. И если наименьшая из них (а это ![]() ) мала, то расчет становится малодостоверным.
) мала, то расчет становится малодостоверным.
Таким образом, по результатам анализа всего двух частично перекрывающихся баз можно составить представление и о полноте каждой из них, и об общем количестве реально существующих документов по теме, в том числе и о количестве документов, отсутствующих в данных базах.
2. Расчет по трем базам
Пусть теперь в нашем распоряжении три БД на одну и ту же тему. В результате анализа их содержимого мы можем получить семь чисел:
|
|
-полное число документов в БД1; |
|
|
-полное число документов в БД2; |
|
|
-полное число документов в БД3; |
|
|
-число документов, имеющихся и в БД1, и в БД2; |
|
|
-число документов, имеющихся и в БД1, и в БД3; |
|
|
-число документов, имеющихся и в БД2, и в БД3; |
|
|
-число документов, имеющихся во всех трех базах. |
Обозначим через
Запишем исходные уравнения:
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
Для получения решения достаточно использовать только четыре уравнения из этих семи, и таких четверок можно составить:
![]() .
.
Иными словами, можно получить 35 комплектов решений. Не все из них равноценны, и вот почему. Относительная точность определения дискретной случайной величины обратно пропорциональна корню квадратному из этой величины (в соответствии с формулами (6)), а в расчетных формулах с умножением и делением таких случайных величин их относительные ошибки суммируются, как показано в выражениях (7). Если учесть, что все n
i, как правило, больше любого из nij, а те, в свою очередь, существенно больше nijk, то отсюда следует, что по возможности следует избегать использования nijk в расчетах, т.е. не пользоваться последним (седьмым) уравнением из набора (10). Тогда число комбинаций уравнений уменьшится до![]() .
.
Эти 15 уравнений можно разделить на 4 группы, в каждой из которых решения получаются циклической перестановкой индексов:
1. Имеются три системы типа:
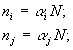 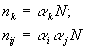 |
Решения: |
2. Имеется шесть систем типа:
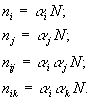 | Решения: |
|
3. Имеется три системы типа:
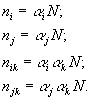 |
Система неразрешима, т.к. уравнения линейно зависимы: |
4. Имеется три системы типа:
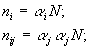 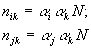 |
Решения: | 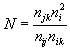 |
Итак, получено 12 комплектов решений, причем расчетные формулы в этих комплектах частично повторяются:
| (5 раз) = | (5 раз) = | (1 раз) = | (1раз); | ||||
| (5 раз) = | (5 раз) = | (1 раз) = | (1раз); | ||||
| (5 раз) = | (5 раз) = | (1 раз) = | (1раз); | ||||
| (3 раза) = | (3 раза) = | (3 раза) = | (1 раз) = | ||||
| = | (1 раз) = | (1 раз). |
При вычислении среднего значения, дисперсии и среднеквадратичного отклонения каждой из этих величин частота повторения формул должна быть учтена введением соответствующих весовых коэффициентов. В простейшем случае расчет усредненных величин можно проводить по формулам:
|
|
(17) |
|
|
(18) |
|
|
(19) |
|
|
(20) |
Дисперсия и среднеквадратичное отклонение для
a1m рассчитываются по формулам (21) и (22), соответственно:|
|
(21) |
|
|
(22) |
Аналогичные формулы можно записать и для остальных трех переменных (мы здесь этого не делаем только из соображений экономии места).
Несмотря на громоздкость приведенных формул, все эти расчеты легко и быстро реализуются в компьютерном исполнении с применением любых электронных таблиц (в данной работе использовались электронные таблицы Excel5.0).
Интересно, что при наличии сведений о трех базах появляется возможность и заглянуть в “кухню” каждого из разработчиков баз. Дело в том, что если исходные данные для расчета представить в несколько иной форме:
|
m1 |
- число документов, присутствующих только в БД1; |
|
m2 |
- число документов, присутствующих только в БД2; |
|
m3 |
- число документов, присутствующих только в БД3; |
|
m12 |
-число документов, имеющихся только в БД1 и в БД2; |
|
m13 |
-число документов, имеющихся только в БД1 и в БД3; |
|
m23 |
-число документов, имеющихся только в БД2 и в БД3; |
|
m123 |
-число документов, имеющихся во всех трех базах, |
то появляется возможность выявить и недобросовестное поведение разработчика, “откачивающего” документы из чужой базы в свою, и обратную ситуацию - наличие мощного источника информации, доступного только одному из разработчиков, и, наконец, наличие некоего “джентльменского набора” документов, обязанных быть представленными в любой базе данных, относящейся к заявленной теме.
Связь между числами m и n очевидна:
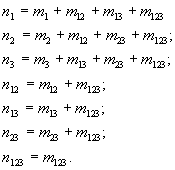 |
(23) |
Естественно считать, что для истинно независимых БД должно бы выполняться условие, что число “тройных совпадений” (т.е. документов, имеющихся во всех трех базах), должно быть меньше любого из трех чисел “двойного совпадения” (это следует из выражения (16)). Если же имеет место ситуация, например, когда база БД1 пополняется из базы БД2, то документы из массива m23 “перекочуют” в массив m123, а из массива m2 в массив m12. В случае наличия уникального источника информации, доступного только для разработчика БД1, например, мы получим аномально высокое значение m1. Наконец, “джентльменский набор” обязан целиком войти в m123, никак не повлияв на содержание остальных исходных данных. И вообще, любое аномальное отклонение какой-либо одной или двух величин несет в себе скрытую информацию о тех или иных технологических особенностях комплектования баз.
3. Модельный эксперимент
Для проверки качества методики расчета был поставлен следующий модельный эксперимент. Допустим, объективно существует массив из N0 документов (например, нормативных актов, регулирующих научно-исследовательскую деятельность). Допустим также, что k разработчиков предлагают свои базы данных по этому вопросу, причем каждый i-й разработчик разыскивает для своей базы эти нормативные акты с заданной вероятностью
ai0, в результате чего в его базе содержится ni0=Nai0 документов соответствующей тематики. Если все числа ni0, nij0 ... в точности соответствуют заданным N0 и ai0 (i=1...k), то, подставив эти числа в формулы, выведенные в предыдущих разделах, мы автоматически реконструируем те величины N0 и ai0, которые сами заложили в модель.А теперь несколько изменим условия модельного эксперимента. Ведь каждая из исходных величин ni, nj ... реально подвержена случаю, и среднеквадратичный разброс их определяется формулами (5), причем в соответствии с теорией вероятности в 80% случаев отклонение реальной величины ni от истинной ni0 не превышает Dni, в 95% случаев это отклонение не превышает 2Dni и лишь в 0,3% случаев отклонение оказывается больше 3Dni. Поэтому модифицируем нашу модель следующим образом: все исходные (“идеальные”) величины х0 (x0= n10, n20, n120 ...) заменяем на
x=x0+ Dx0(f-w)A,
где
Dx0=А - масштабный коэффициент, задающий амплитуду случайного воздействия (А= 0...4).
Подставляя эти измененные исходные величины в наши расчетные формулы, мы, естественно, получим результат, в какой-то степени близкий к “идеальному”, но все же от него отличающийся. Для оценки точности реконструирования параметров N0 и ai0 модельный эксперимент данного типа можно повторять неоднократно, каждый раз с помощью генератора случайных чисел варьируя набор исходных данных. Это и было выполнено для двух моделей:
1. Две базы при N0=600, a10=0,5 и a20=0,333.
2. Три базы при N0=1000, a10=0,3, a20=0,5 и a30=0,6.
Чтобы ощутить масштаб отклонений исходных величин в каждой серии экспериментов, в таблицах 2 и 3 показана часть результатов (вся серия включала по 60 экспериментов для каждого значения амплитуды А).
Таблица 2. Исходные числа для модельного эксперимента с двумя базами
(n1=300, n2=200, n12=100)
| А=1 | n1 |
295 |
307 |
297 |
294 |
... |
n2 |
196 |
208 |
194 |
195 |
... |
|
n12 |
100 |
106 |
99 |
96 |
... |
|
| А=2 | n1 |
300 |
287 |
319 |
321 |
... |
n2 |
187 |
205 |
200 |
194 |
... |
|
n12 |
85 |
104 |
110 |
98 |
... |
|
| А=3 | n1 |
331 |
302 |
324 |
273 |
... |
n2 |
188 |
192 |
203 |
176 |
... |
|
n12 |
114 |
93 |
107 |
75 |
... |
Таблица 3. Исходные числа для модельного эксперимента с тремя базами
(n1=300, n2=500, n3=600, n12=150, n13=180, n23=300, n123=90)
| А=1 | n1 |
297 |
306 |
304 |
309 |
... |
n2 |
495 |
488 |
508 |
495 |
... |
|
n3 |
581 |
599 |
611 |
600 |
... |
|
n12 |
148 |
152 |
150 |
154 |
... |
|
n13 |
178 |
182 |
179 |
190 |
... |
|
n23 |
291 |
297 |
298 |
294 |
... |
|
n123 |
87 |
91 |
86 |
98 |
... |
|
| А=2 | n1 |
287 |
324 |
277 |
302 |
... |
n2 |
478 |
534 |
477 |
470 |
... |
|
n3 |
571 |
596 |
603 |
570 |
... |
|
n12 |
152 |
170 |
138 |
161 |
... |
|
n13 |
172 |
184 |
175 |
174 |
... |
|
n23 |
299 |
322 |
307 |
278 |
... |
|
n123 |
100 |
102 |
91 |
91 |
... |
|
| А=3 | n1 |
312 |
283 |
313 |
300 |
... |
n2 |
524 |
491 |
526 |
557 |
... |
|
n3 |
565 |
617 |
601 |
622 |
... |
|
n12 |
164 |
138 |
158 |
167 |
... |
|
n13 |
177 |
176 |
196 |
186 |
... |
|
n23 |
304 |
298 |
313 |
324 |
... |
|
n123 |
90 |
81 |
96 |
103 |
... |
|
| А=4 | n1 |
304 |
290 |
303 |
295 |
... |
n2 |
497 |
507 |
490 |
497 |
... |
|
n3 |
586 |
624 |
583 |
640 |
... |
|
n12 |
149 |
139 |
143 |
156 |
... |
|
n13 |
195 |
160 |
167 |
190 |
... |
|
n23 |
303 |
318 |
283 |
312 |
... |
|
n123 |
104 |
79 |
80 |
98 |
... |
Для модели двух баз с “теоретическими” значениями N0=600,
a10=0,5 и a20=0,333 шестьдесят пробных расчетов с учетом случайного фактора дали следующий результат (см. таблицу 4):Таблица 4. Результаты модельного эксперимента с двумя базами данных при
N0=600, a10=0,5 и a20=0,333| Параметры | Среднее по серии | Ошибка каждой модели, % |
Максимальное значение в серии |
Максимальное значение в серии |
|
| А=1 | a 1 |
0,502 |
12 |
0,53 |
0,47 |
a 2 |
0,334 |
11-12 |
0,36 |
0,31 |
|
N |
600 |
13-14 |
632 |
561 |
|
| А=2 | a 1 |
0,508 |
12-13 |
0,575265 |
0,45 |
a 2 |
0,34 |
11-12 |
0,393888 |
0,30 |
|
N |
593 |
13-14 |
683 |
531 |
|
| А=3 | a 1 |
0,497 |
11-14 |
0,607819 |
0,38 |
a 2 |
0,34 |
13-15 |
0,400815 |
0,26 |
|
N |
600 |
13-15 |
703 |
494 |
|
В этой таблице во втором столбце помещены наименования искомых величин, в третьем - среднее по серии из 60 экспериментов значение каждой величины, в четвертом столбце - расчетная ошибка единичного измерения, в последних двух столбцах - максимальное и минимальное значение искомой величины, случившееся в серии.
Видно, что даже в случае А=3 (вероятность максимального отклонения при таком А в теории оценивается в 0,3%) результаты расчета очень неплохие. Числа четвертого столбца, соответствующие средней ошибке каждого единичного расчета, определяют допустимый разброс, намного перекрывающий отклонение любой из средних величин (третий столбец) от “теоретической”. Для второй серии измерений (при А=2) ошибка единичного расчета ближе всего соответствует максимальному и минимальному отклонениям расчетных величин от средних (а вероятность такого экстремального отклонения теорией определяется в 5%). Средние же величины, полученные в этой серии, совпадают с теоретическими с точностью до долей процента. И только в третьей серии экспериментов с сильно завышенной величиной разброса (вероятность такой ситуации оценивается всего в 0,3%) случаются варианты, когда реконструированные величины более чем на 20% отличаются от истинных (хотя средние по серии значения попрежнему очень близки к истинным).
Эксперимент с тремя базами дал результаты, сводка которых приведена в Таблице 5.
Таблица 5. Результаты модельного эксперимента с тремя базами данных
(n1=300, n2=500, n3=600, n12=150, n13=180, n23=300, n123=90)
| Параметры | Среднее по серии | Ошибка каждой модели, % |
Максимальное значение в серии |
Максимальное значение в серии |
|
| А=1 | a 1 |
0,30 |
0,5-1,5 |
0,32 |
0,28 |
a 2 |
0,50 |
0,8-1,5 |
0,52 |
0,48 |
|
a 3 |
0,60 |
0,4-1,3 |
0,63 |
0,57 |
|
N |
998 |
0,1-1,2 |
1036 |
966 |
|
| А=2 | a 1 |
0,30 |
1,5-3 |
0,33 |
0,26 |
a 2 |
0,50 |
1-4 |
0,53 |
0,46 |
|
a 3 |
0,60 |
1-3,5 |
0,64 |
0,55 |
|
N |
999 |
0,5-3 |
1495 |
926 |
|
| А=3 | a 1 |
0,30 |
2-6 |
0,35 |
0,24 |
a 2 |
0,49 |
1-7 |
0,56 |
0,42 |
|
a 3 |
0,60 |
0,5-5 |
0,66 |
0,54 |
|
N |
1012 |
1-5 |
1138 |
886 |
|
| А=4 | a 1 |
0,300 |
2-10 |
0,37 |
0,25 |
a 2 |
0,50 |
2-11 |
0,57 |
0,43 |
|
a 3 |
0,60 |
2-6 |
0,67 |
0,51 |
|
N |
998 |
2-9 |
1167 |
863 |
|
Все выводы, полученные на модели двух баз, здесь справедливы даже в усиленном виде. Поэтому мы решились на расширение эксперимента в сторону еще большей “раскачки” исходных данных. Случайно такая раскачка уже практически не может произойти, но комплектование баз - процесс не чисто статистический и нельзя исключить возможность как негласного использования содержимого чужих баз, так и частного доступа к богатому информацией первоисточнику (например, к архиву мощного эмитента документов); кроме того, неизбежно и влияние ненулевого “джентльменского набора” документов, обязательных во всех базах (более подробно этот фактор будет рассмотрен ниже). Четвертая серия экспериментов показала, что и в этом случае максимальное отклонение реконструированных величин от точных значений укладывается в 15-25%.
В этой группе экспериментов проявилась не слишком заметная особенность: чем меньше величина ai, тем больше оказывается разброс реконструированной величины этого параметра. Если теперь вернуться к данным Таблицы 5 для двух баз, то и там можно заметить ту же тенденцию.
4. Три базы и “джентльменский набор”
Выше упоминалось, что, кроме чисто статистических механизмов комплектования баз данных, существует некоторое количество документов, являющихся “индикаторами” тематики базы данных. Например, едва ли кто осмелится назвать базу правовой информации наименованием “Федеральное законодательство России”, если в этой базе будет отсутствовать такой документ, как Конституция РФ. Или если в базе данных “Неорганические материалы” будут отсутствовать сведения о простых химических элементах (не соединениях, а именно элементах). С точки зрения задач настоящей работы существование “джентльменского набора” обязательных документов добавляет еще одно неизвестное к нашим четырем и избыточность системы уравнений (10)-(16) уменьшается. Но при этом существенную роль начинает играть именно последнее из этих уравнений, т.к. именно там в максимальной степени сказывается влияние новой неизвестной величины. И сами уравнения с учетом этой неизвестной выглядят теперь несколько иначе:
|
|
|
Если принять тот же способ решения этой системы уравнений, т.е. составлять из семи уравнений возможные комбинации по пять, то в нашем распоряжении оказывается
| комбинация уравнений. Можно, как и раньше, распределить их по следующим группам: |
1. Имеются три системы типа:
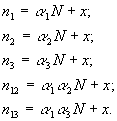 |
Решение: | 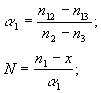 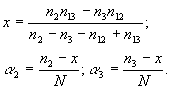 |
2. Имеются три системы типа:
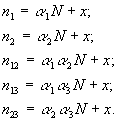 |
Решение: | 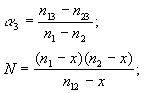 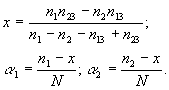 |
3. Имеются три системы типа:
Простых решений не видно, а сложные подстановки дадут слишком большую ошибку результата, поэтому эта группа систем исключается из рассмотрения. 4. Имеются шесть систем типа: 5. Имеются три системы типа: Итак, из перечисленных систем можно получить 18 частных решений (учитывающих только часть уравнений общей системы (24)-(30)). Не загромождая текст формулами для вычисления средних значений, дисперсии и среднеквадратичной ошибки, скажем только, что все эти вычисления производятся по той же методике. что и в разделе 3 настоящей работы, оформлены они также в форме электронных таблиц Excel5.0. Расчетные формулы настоящего раздела несколько сложнее, чем в разделе 3, поэтому интересно было проверить, насколько хороша сходимость и устойчивость решений при учете “джентльменского набора” документов, для чего был вновь поставлен модельный эксперимент, описанный в следующем разделе. 5. Модельный эксперимент-2
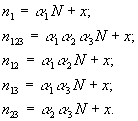
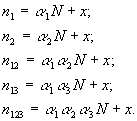
Решение:
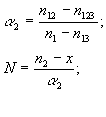
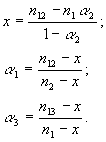
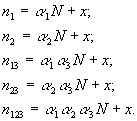
Решение:
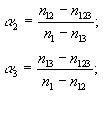
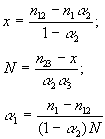
Исходные посылки модельного эксперимента таковы. Объективно существует массив из N0 документов по заданной теме, причем Y0 документов из этого количества являются общедоступными и обязательными для любой базы данных, претендующих на обслуживание именно этой темы. Таким образом, каждый из k разработчиков имеет в своей базе эти Y0 документов, а остальные документы, как и раньше, разыскивает и включает в свою базу с вероятностью ai0, так что в его базе содержится
ni0=Y0+(N0 -Y0)ai0 документов. Фактор случайности учтем точно так же, как это было сделано в разделе 3, т.е. все исходные (“идеальные”) величины х0 (x0=n10,n20,n120 ...) заменяем на x=x0+ Dx0(f-w)A,
где Dx0= Поскольку минимальное количество баз данных в этом случае не может быть меньше трех (при двух базах получается три уравнения с четырьмя неизвестными и система уравнений получается недостаточной), то в данном разделе исследовалась только одна модель со следующими исходными данными: N0=1050, Y0=50, a10=0,3, a20=0,5 и a30=0,7. Каждая серия включала 100 модельных экспериментов при фиксированном значении масштабного коэффициента А. В таблице 6 приведены исходные данные первых экспериментов этих серий. Таблица 6. Исходные числа для модельного эксперимента с тремя базами n1 360 350 352 346 347 345 348 354 ... n2 572 650 567 539 545 538 546 549 ... n3 766 750 750 731 755 743 734 754 ... n12 203 200 205 200 199 196 200 201 ... n13 269 257 261 253 261 255 262 266 ... n23 413 404 408 382 401 395 393 399 ... n123 156 157 157 150 158 152 157 155 ... n1 368 354 368 366 334 342 355 351 ... n2 588 565 516 573 550 548 561 566 ... n3 773 762 765 791 787 730 764 736 ... n12 205 211 202 227 187 201 210 202 ... n13 277 258 277 274 251 248 258 251 ... n23 437 409 379 426 407 398 420 406 ... n123 168 159 159 181 147 153 160 154 ... n1 336 350 300 402 377 392 407 351 ... n2 573 592 501 553 550 583 544 613 ... n3 781 707 716 847 781 748 709 776 ... n12 192 225 187 231 225 216 227 220 ... n13 251 252 222 302 277 289 299 267 ... n23 392 416 374 445 394 425 387 450 ... n123 138 183 148 202 169 169 184 168 ... n1 337 352 350 344 358 361 348 342 ... n2 559 557 554 550 554 543 553 536 ... n3 772 765 754 752 758 758 755 738 ... n12 193 201 200 196 203 205 204 195 ... n13 259 258 262 257 270 270 261 251 ... n23 413 404 410 399 403 397 408 392 ... n123 153 156 159 153 161 159 158 148 ... Результаты модельного эксперимента (см. Таблицу 7) показали, что в данном случае статистический разброс исходных данных влияет на расчет гораздо сильнее. Повсеместное участие всевозможных вычитаний в формулах в сочетании с делением и умножением значительно увеличивает относительную ошибку результата, а иногда делает расчет просто невозможным или бессмысленным (деление на ноль, отрицательные значения эффективности, и т.п.). Все такие ситуации были отнесены к неудачам расчета и сведены в последний столбец таблицы 7. Таблица 7. Сводка результатов модельного эксперимента Среднее значение Среднекв. ошибка Миним. значение Максим. значение Процент неудач 0,30 0,010 0,27 0,32 0 0,50 0,011 0,47 0,52 0 0,70 0,012 0,66 0,72 0 Y 50 8 31 66 0 N 1056 16 1012 1106 0 0,30 0,02 0,25 0,35 0 0,50 0,025 0,43 0,54 0 0,70 0,031 0,62 0,75 0 Y 48 16 12 83 0 N 1073 74 974 1630 0 0,29 0,066 0,23 0,38 3 0,48 0,12 0,30 0,56 4 0,70 0,10 0,27 0,82 1 Y 59 22 17 110 0 N 1194 552 871 4992 0 0,30 0,21 -0,54 1,08 31 0,53 0,34 0,30 1,00 40 0,71 0,26 0,35 1,07 12 Y 112 166 0 1381 1 N 1292 937 601 7596 0 Анализируя данные Таблицы 7, можно сделать следующие выводы: 1. В 80% случаев (А=1) точность определения искомых величин достаточно высока: ошибка определения эффективностей a в среднем составляет 1,5-3%, и даже максимальные отклонения в серии из 100 экспериментов укладываются в 6-10%; величина “джентльменского набора” документов Y определяется менее точно (среднеквадратичная ошибка составляет 15%, но максимальное отклонение в серии достигло 30-40%), впрочем, на точности определения полного числа документов N это почти не сказывается, 1,5%-ная ошибка в среднем и 4-5% в максимальном отклонении - вполне удовлетворительно. 2. Увеличение А до 1,5 увеличивает ошибку определения всех величин, хотя средние значения остаются весьма близки к “идеальным”. Наиболее чувствительно отреагировала на рост статистического разброса все та же величина Y. Заметим, что в обеих сериях все без исключения расчеты прошли корректно, никаких сбоев типа деления на ноль не было (хотя в знаменателе иногда появлялись аномально маленькие величины, о чем свидетельствует несимметричность максимальных отклонений N в сторону больших и малых значений). 3. Увеличение А до двух заметно ухудшило условия расчета: средние значения искомых величин уже существенно отличаются от “идеальных”, появились сбои в расчете, появились и аномально большие Nмакс, и отрицательные величины a (в таблице они изъяты), среднеквадратичные ошибки уже выросли до 30-50%. 4. Последняя серия (А=3) показала, что такой разброс (а вероятность его самопроизвольной реализации не превышает 0,3%) делает расчет бессмысленным: 40% экспериментов этой серии не дали результата, расчетные формулы не работали. Такой результат позволяет сделать вывод, что для баз с независимыми и одинаковыми технологиями комплектации расчет по данному алгоритму даст разумные результаты, статистический разброс исходных данных слабо влияет на конечные результаты; однако, любая взаимозависимость баз или любая исключительность какой-либо базы обязательно скажутся на корректности расчета и скорее всего в какой-либо из расчетных формул приведут к бессмыслице. Очевидно, чтобы из таких ситуаций сделать определенные и вполне конкретные выводы, необходимо предварительно промоделировать некоторые наиболее простые варианты. ![]() -среднеквадратичная ошибка,
f и w - случайные числа с равномерным распределением в интервале от нуля до единицы,
А - масштабный коэффициент, задающий амплитуду случайного воздействия (А= 0...3).
-среднеквадратичная ошибка,
f и w - случайные числа с равномерным распределением в интервале от нуля до единицы,
А - масштабный коэффициент, задающий амплитуду случайного воздействия (А= 0...3).
(точные значения составляют: n1=350, n2=550, n3=750, n12=200, n13=260, n23=400, n123=155)
А=1
А=1,5
А=2
А=3
(исходные данные N0=1050, Y0=50, a10=0,3, a20=0,5 и a30=0,7)
А=1
a1
a2
a3
А=1,5
a1
a2
a3
А=2
a1
a2
a3
А=3
a1
a2
a3